RF 트랜스포머의 애플리케이션
RF 트랜스포머는 전자 회로에서 다음과 같은 용도로 널리 사용됩니다:
- 최대 전력 전송을 달성하고 원하지 않는 신호 반사를 억제하기 위한 임피던스 매칭
- 전압, 전류 승압 또는 강압
- 효율적인 AC 전송을 제공하면서 회로 간 DC 절연
- 평형 회로와 불평형 회로 간의 인터페이스(예: 평형 증폭기)
트랜스포머 회로 및 임피던스 관계
신호 전류가 1차 권선을 통과하면 자기장이 발생하여 2차 권선에 전압이 유도됩니다. 2차에 부하를 연결하면 부하에 AC 전류가 흐르게 됩니다.
일반적으로 RF 신호 경로의 종단 임피던스를 제어해야 하며, 특히 경로 길이가 파장에 비해 무시할 수 없는 광대역 애플리케이션에서 그렇습니다. 광대역 RF 트랜스포머는 전송선처럼 동작하는 꼬인 와이어를 사용하여 감겨 있으며, 필요한 결합은 이러한 라인의 길이를 따라 그리고 코어를 통해 자기적으로 발생합니다. 1차 및 2차 권선이 트랜스포머가 설계된 저항성 종단 임피던스에 연결될 때 최적의 성능이 달성됩니다. 예를 들어, 1:1의 턴 비율을 가진 트랜스포머는 일반적으로 50옴 또는 75옴 시스템에서 사용하도록 설계됩니다.
이 애플리케이션 노트에서는 사용자가 성능 테스트와 실제 사용 모두에서 트랜스포머에 제공해야 하는 종단 임피던스에 대해 지속적으로 언급합니다. 논의의 일관성을 위해, 1:1보다 큰 턴 비율을 가진 트랜스포머는 승압으로 설명됩니다. 즉, 2차 임피던스가 1차 임피던스보다 큽니다. 그러나 실제 사용에서는 필요에 따라 승압 또는 강압으로 연결할 수 있습니다.
V_2 = N V_1 \quad \text{and} \quad I_2 = \frac{I_1}{N}, \quad \text{where } N \text{ is the turns ratio} \\[1.5ex]
Z_2 = \frac{V_2}{I_2} \quad \text{and} \quad Z_1 = \frac{V_1}{I_1}, \quad \text{therefore } Z_2 = N^2 Z_1즉, 임피던스 비율은 턴 비율의 제곱입니다.
그림 1c의 2차 권선에는 센터 탭이 있어 트랜스포머를 평형 신호 분배기로 유용하게 사용할 수 있습니다. 이 구성을 가진 잘 설계된 RF 트랜스포머로 우수한 진폭 및 위상 밸런스를 얻을 수 있습니다.
다음의 그림 1c에 대한 방정식에서 턴 비율 N은 전체 2차 권선을 나타냅니다.
V_4 = NV_1, \quad \text{and} \quad V_2 = V_3 = N\frac{V_1}{2}2차의 두 절반이 동일한 종단 임피던스 Z2 및 Z3에 연결되면,
I_2 = I_3 = \frac{I_1}{N}; \quad Z_4 = N^2 Z_1, \\\text{and} \quad Z_2 = Z_3 = \frac{Z_4}{2} = N^2 \frac{Z_1}{2}그림 1c 트랜스포머의 변형으로, 고주파 성능에 유리한 것이 그림 2에 나와 있습니다. 센터 탭 트랜스포머 입력에서 불평형 신호를 평형으로 변환하기 위해 입력에 전송선 트랜스포머를 캐스케이드로 추가합니다. 이 설계의 특징:
- 1000 MHz를 초과하는 넓은 대역폭
- 우수한 진폭 및 위상 밸런스
- 1차 측에서 더 높은 반사 손실(더 낮은 VSWR)
트랜스포머 성능 특성
삽입 손실 및 주파수 대역폭
트랜스포머의 삽입 손실은 동일한 턴 비율을 가진 이상적인(이론적으로 무손실) 트랜스포머 대신 임피던스 매칭된 전송 시스템에 트랜스포머를 삽입했을 때 손실되는 입력 전력의 비율입니다. 실제 삽입 손실은 트랜스포머 권선의 비이상적 특성 임피던스와 권선 및 코어 손실에 의해 영향을 받습니다.
주파수에 따른 일반적인 삽입 손실 변화는 그림 3에 설명되어 있으며, 일반적으로 지정되는 대로 중간 대역 손실을 기준으로 1 dB, 2 dB 및 3 dB 대역폭을 보여줍니다. 저주파에서의 삽입 손실은 병렬(자화) 인덕턴스에 의해 영향을 받습니다. 저온에서는 자성 코어의 투자율 감소로 인해 저주파 삽입 손실이 증가하는 경향이 있습니다. 고주파 삽입 손실은 권선 간 커패시턴스, 직렬(누설) 인덕턴스, 코어 및 도체 손실에 기인합니다. 고온에서는 코어 투자율의 손실 성분 증가로 인해 더 커지는 경향이 있습니다.
트랜스포머 삽입 손실에 대한 또 다른 영향은 높은 AC 또는 DC 전류입니다. 대부분의 RF 트랜스포머는 일반적으로 최대 250 mW의 RF 또는 30 mA의 불평형 DC 전류가 권선을 통과하는 소신호 애플리케이션에서 사용됩니다. 작은 크기와 가장 넓은 대역폭을 위해 실용적으로 가장 작은 크기의 코어가 사용됩니다. 더 큰 RF 전력 또는 DC 전류가 적용된 상태에서 삽입 손실 사양을 충족해야 하는 경우, 자성 코어의 포화 및 결과적인 대역폭 감소를 방지하기 위해 트랜스포머 설계에서 이를 고려해야 합니다.
트랜스포머의 삽입 손실은 어떻게 측정합니까? 이 질문은 1:1 이외의 임피던스 비율에서 특히 적절한데, 일반적으로 일정한 50 또는 75옴인 테스트 장비의 임피던스를 수용해야 하기 때문입니다. 세 가지 방법이 있습니다:
- 세 개의 트랜스포머를 쌍으로 테스트합니다: A와 B, A와 C, B와 C. 각 쌍은 백투백으로 측정됩니다. 즉, 고임피던스 권선이 서로 직접 연결되고 저임피던스 권선이 트랜스포머 임피던스와 일치하는 장비의 소스와 검출기를 향합니다. 이것은 3개의 결합 삽입 손실 값을 생성하므로 3개의 미지수(개별 A, B, C 삽입 손실) 값을 계산할 수 있습니다.
- 트랜스포머는 고임피던스 권선과 장비 사이에 연결된 매칭 회로로서 최소 손실 패드와 함께 개별적으로 측정됩니다. 이것은 매칭 패드를 쉽게 사용할 수 있는 50옴에서 75옴 트랜스포머를 테스트하는 데 실용적인 것으로 밝혀졌습니다. 매칭 회로의 손실(dB)은 측정값에서 빼서 트랜스포머 자체의 삽입 손실을 얻어야 합니다. 이 방법은 2차에 2개의 연결만 이루어지는 경우에 적용됩니다. 그림 4는 이 방법으로 테스트한 50옴에서 75옴 트랜스포머 모델 TC1.5-1의 성능을 보여줍니다. 매칭 패드의 손실은 두 개를 백투백으로 측정하고 dB 값을 2로 나누어 결정했습니다.
- 트랜스포머에 센터 탭 2차 권선이 있는 경우 180도 전력 분배기로 연결할 수 있습니다. 2차의 각 절반은 그림 1c에 대해 주어진 방정식을 참조하여 매칭 임피던스 N2 Z / 2로 종단되어야 합니다. 이것은 트랜스포머와 삽입 손실 장비의 감지 테스트 포트 사이에 매칭 네트워크를 사용해야 합니다. 개별 테스트 포트는 하나의 출력만 보기 때문에 분할에 대한 3 dB와 매칭 네트워크의 손실 모두 측정된 삽입 손실 값에서 빼야 합니다. 두 출력을 모두 감지하면 이 방법으로 진폭 및 위상 불균형도 측정할 수 있습니다. 매칭 네트워크의 요소 값과 손실은 표 1에 나열되어 있습니다.
참고: 적절한 소스 종단이 필요한 장비가 이 방법에서 하나 또는 두 출력에 연결되므로 매칭 네트워크에 특별한 설계 고려 사항이 적용되며 최소 손실 패드가 되어서는 안 됩니다. 이것은 센터 탭 트랜스포머의 진폭 및 위상 밸런스 측정이라는 제목의 섹션에서 자세히 논의되며, 적합한 매칭 네트워크에 대한 설계 기준, 요소 값 및 삽입 손실이 제공됩니다.
이 방법이 광범위한 임피던스 비율(N2 값)을 가진 센터 탭 트랜스포머에 유용하다는 것을 보여주기 위해, 다음 모델에 대한 주파수 대 삽입 손실이 그림 5, 6 및 7에 나와 있습니다:
실제 중간 대역 삽입 손실은 각 그래프 위에 표시되어 있습니다.
임피던스 및 반사 손실
2차 권선을 들여다본 임피던스는 1차 권선이 지정된 임피던스(일반적으로 50 또는 75옴)로 종단된 상태에서 측정되며, 이론적 종단 값(그림 1의 Z1, Z2 또는 Z3)과 비교됩니다.
반사 손실 또는 VSWR은 2차가 이론적 임피던스로 종단된 상태에서 1차 권선에서 측정됩니다. 예: 1:2 임피던스 비율(1:1.414 턴 비율) 1차 트랜스포머의 경우 2 x Zprimary.
트랜스포머의 물리적 파라미터
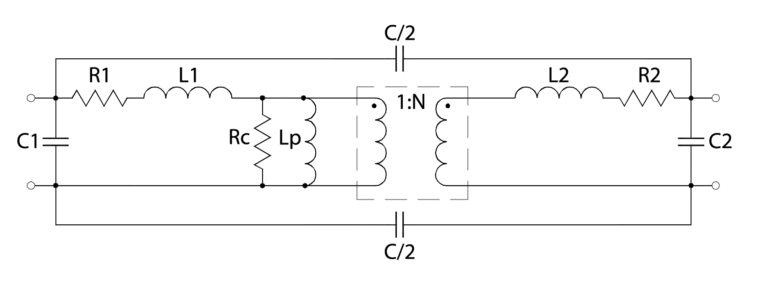
RF 트랜스포머의 성능은 그림 8의 등가 회로를 통해 이해할 수 있습니다:
- L1 및 L2는 두 권선 간의 불완전한 자기 결합으로 인한 1차 및 2차 누설 인덕턴스입니다. 리액턴스가 주파수에 비례하기 때문에 이러한 인덕턴스는 고주파에서 삽입 손실을 증가시키고 반사 손실을 감소시킵니다.
- R1 및 R2는 1차 및 2차 권선의 저항 또는 구리 손실입니다. 표피 효과는 고주파에서 저항을 증가시켜 삽입 손실 증가에 기여합니다.
- 권선 내 커패시턴스 C1 및 C2, 그리고 권선 간 커패시턴스 C도 고주파에서 성능 제한에 기여합니다. 그러나 RF 트랜스포머에 사용되는 전송선 설계의 뚜렷한 장점은 권선 간 커패시턴스의 상당 부분이 누설 인덕턴스(병렬 커패시턴스 및 직렬 인덕턴스)와 함께 전송선 파라미터에 흡수되어 기존 트랜스포머 권선으로 얻을 수 있는 것보다 훨씬 넓은 대역폭을 제공한다는 것입니다.
- Lp는 트랜스포머의 저주파 성능을 제한하는 자화 인덕턴스입니다. 이것은 자성 코어의 투자율과 단면적, 그리고 턴 수에 의해 결정됩니다. 저주파에서 삽입 손실이 증가하고 반사 손실이 감소합니다. 또한 많은 코어 재료의 투자율은 온도가 감소하면 감소하고 실온 이상에서는 증가합니다. 이것은 위에서 설명한 대로 그림 3의 삽입 손실 곡선의 저주파 부분이 퍼지는 원인입니다.
- 커패시턴스와 누설 인덕턴스의 온도 변화는 비교적 작습니다. 권선 저항은 온도에 따라 증가하며 그림 3의 곡선의 고주파 부분이 퍼지는 데 기여합니다.
- 저항 Rc는 코어 손실을 나타냅니다. 일반적으로 이 손실에는 세 가지 기여가 있습니다:
- 와전류 손실, 주파수에 따라 증가
- 히스테리시스 손실, 자속 밀도(적용된 신호 레벨)에 따라 증가
- 잔류 손실, 부분적으로 자기 회전 공명에 기인
적용된 RF 신호가 관성과 마찰을 가진 입자처럼 동작하는 코어 재료의 자기 도메인에 진동 운동을 일으키는 것으로 그릴 수 있습니다. 따라서 이 운동은 에너지 손실을 유발합니다. 고주파 신호는 더 빠른 운동을 유발하여 더 큰 코어 손실을 초래하며, 이것은 Rc 값의 감소로 나타납니다. 고온에서는 무작위 열 진동이 더 커지고 자기 도메인의 움직임을 제어하기 위해 RF 신호가 소비해야 하는 에너지에 추가됩니다. 따라서 코어 손실은 고주파에서 삽입 손실 증가와 반사 손실 감소에 기여합니다. 이러한 효과는 그림 3에 표시된 것처럼 고온에서 더욱 두드러집니다.
진폭 및 위상 밸런스 측정: 센터 탭 트랜스포머
정의
- 진폭 밸런스, 때때로 진폭 “불균형”이라고 하며, 센터 탭을 접지 기준으로 사용하는 센터 탭 트랜스포머의 두 출력 간 신호 진폭 차이의 절대값(dB)입니다.
- 위상 밸런스, 때때로 위상 “불균형”이라고 하며, 180도 공칭 위상 분할 값을 뺀 후 센터 탭을 접지 기준으로 사용하는 센터 탭 트랜스포머의 두 출력 간 신호 위상 차이의 절대값입니다.
측정 방법: 트랜스포머 2차의 각 절반과 테스트 장비의 감지 포트 사이의 매칭 네트워크
삽입 손실 측정에 관한 섹션의 끝 부분에서 센터 탭 2차가 있는 트랜스포머를 전력 분배기처럼 테스트할 수 있다고 언급했습니다. 그러나 고려해야 할 차이점이 있습니다: 전력 분배기로 제작된 장치는 출력 간에 격리를 제공하는 내부 회로가 있습니다. 이 조항은 다른 출력의 부하와 관계없이 각 출력 포트를 들여다본 일정한 임피던스를 보장합니다. 반면에 트랜스포머는 더 단순한 장치이므로 격리가 부족합니다. 따라서 매칭 네트워크의 설계는 1차 대 절반 2차 비율에 의해 변환된 1차 소스 임피던스뿐만 아니라 이와 병렬로 있는 또 다른 임피던스, 즉 다른 절반 2차 권선을 종단하는 것의 입력 임피던스도 고려해야 합니다.
상황은 그림 9에 설명되어 있습니다. Rt는 테스트 장비의 소스 및 감지 포트 임피던스이며, 트랜스포머의 1차가 설계된 임피던스이기도 합니다. 전체 2차는 N2Rt로 종단되어야 합니다. 따라서 각 매칭 네트워크는 출력이 Rt로 종단된 상태에서 입력 임피던스가 N2Rt ÷ 2이어야 합니다.
각 매칭 네트워크의 출력 소스 임피던스는 부하 Rt를 나타내는 케이블에 공급해야 하므로 Rt와 같아야 합니다. 이것은 매칭 네트워크가 다음 두 임피던스의 병렬 조합인 소스 임피던스에서 공급되는 동안이어야 합니다: 하나는 절반 2차에서 (N ÷ 2)2Rt로 나타나는 변환된 소스 임피던스 R입니다. 다른 하나는 한 절반 2차에서 다른 절반 2차로 결합된 다른 매칭 네트워크의 입력인 N2Rt ÷ 2입니다. 결과는 N2Rt ÷ 6입니다.
매칭 네트워크에 대한 임피던스 제약 조건은 그림 10a에서 10c에 표시된 것처럼 트랜스포머 임피던스 비율 N2의 값에 따라 세 가지 토폴로지가 필요합니다:
두 가지 비자명 케이스 10a와 10c 각각에 대해, 네트워크의 입력 및 출력 임피던스에 대한 요구 사항은 두 개의 미지수 Rs와 Rp를 풀기 위한 두 개의 방정식을 제공합니다. N2 < 3의 경우, 그림 10a를 참조하면, 방정식은 다음과 같습니다:
(R_t + R_s) \parallel R_p = \frac{N^2}{2} R_t \quad \text{and}\\\left(\frac{N^2}{6}R_t\right) \parallel R_p + R_s = R_t
해는 다음과 같습니다:
R_s = R_t \sqrt{1 - \frac{N^2}{4}}R_p = R_t \frac{\frac{N^2}{2}\left(\sqrt{1 - \frac{N^2}{4}} + 1\right)}{\sqrt{1 - \frac{N^2}{4}} + 1 - \frac{N^2}{2}}
N2 > 3의 경우, 그림 10c를 참조하면, 방정식은 다음과 같습니다:
R_p \parallel R_t + R_s = \frac{N^2}{2} R_t \quad \text{and}\\ \quad \left(\frac{N^2}{6} R_t + R_s\right) \parallel R_p = R_t
해는 다음과 같습니다:
R_s = R_t \left( \frac{N}{\sqrt{3}} \sqrt{\frac{N^2}{3} - 1} + \frac{N^2}{6} \right)
R_p = R_t \sqrt{\frac{N^2}{3} \left/ \left(\frac{N^2}{3} - 1\right)\right.}
N2 = 3의 경우, Rs = Rt ÷ 2이고 Rp는 무한대입니다.
정확한 RF 위상 밸런스 측정을 위해 매칭 네트워크의 구성과 연결은 회로의 두 절반 간에 전기적 대칭을 제공해야 합니다.
위 방법의 효과를 보여주기 위해 트랜스포머의 진폭 및 위상 불균형을 테스트하는 데 사용되었으며, 결과는 그림 11, 12 및 13에 나와 있습니다. 이들은 그림 5, 6 및 7에서 삽입 손실이 제공된 것과 동일한 트랜스포머입니다.
남은 작업은 매칭 네트워크의 삽입 손실에 대한 표현식을 유도하여 위에서 설명한 “전력 분배기” 방법으로 테스트할 때 센터 탭 트랜스포머 자체의 삽입 손실을 얻기 위해 측정값에서 뺄 수 있도록 하는 것입니다. 다시 말하지만, 3 dB(분할에 대한)도 측정값에서 빼야 합니다.
그림 14는 2차가 매칭된 저항성 임피던스로 종단된 트랜스포머의 전압 관계를 보여줍니다.
1차를 들여다본 임피던스가 Rt이므로 1차 양단의 전압은 개방 회로 소스 전압 Vi의 절반입니다. 각 종단 저항에 전달되는 전력은 전압의 제곱을 저항으로 나눈 값입니다:
P_o = \frac{\left(\frac{NV_i}{4}\right)^2}{\frac{N^2}{2}R_t} = \frac{V_i^2}{8R_t}
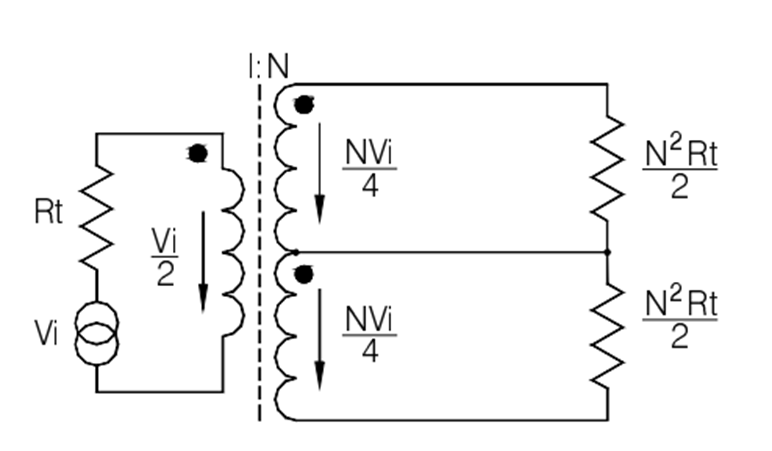
그림 15는 다양한 매칭 네트워크가 절반 2차 뒤에 삽입되고 그림 10에 따른 매칭 부하가 장비의 센서 포트를 나타내는 Rt로 대체될 때 어떤 일이 발생하는지 보여줍니다.
그림 15: 전력 계산을 위한 전압 관계
그림 15a는 그림 10a의 “N2 < 3″ 매칭 네트워크를 포함합니다. 부하 Rt에 전달되는 전력은 POL입니다(아래 첨자 L은 낮은 N2 케이스를 나타냄):
P_{OL} = \left(\frac{R_t}{R_t + R_s}\right)^2 \left(\frac{N^2 V_i^2}{16 R_t}\right) = \frac{R_t N^2 V_i^2}{16(R_t + R_s)^2}
\text{Loss} = \frac{P_O}{P_{OL}} = 2 \frac{(R_t + R_s)^2}{N^2 R_t^2}그림 15b는 그림 10b에 따른 N2 = 3 케이스를 보여줍니다:
P_{O3} = \frac{V_i^2}{12 R_t}\text{Loss} = \frac{P_O}{P_{O3}} = 1.5그림 15c는 그림 10c에 해당하는 N2 > 3에 대한 것입니다(POH의 아래 첨자 H는 높은 N2 케이스를 나타냄):
P_{OH} = \left(\frac{R_p R_t}{R_p R_t + R_p R_s + R_t R_s}\right)^2 \left(\frac{N^2 V_i^2}{16 R_t}\right)
\text{Loss} = \frac{P_O}{P_{OH}} = 2 \frac{(R_p R_t + R_p R_s + R_t R_s)^2}{N^2 R_p^2 R_t^2}표 1은 Mini-Circuits가 센터 탭 RF 트랜스포머를 제공하는 임피던스 비율 값에 대해 Rt로 정규화된 매칭 네트워크 저항 값과 네트워크 손실(dB)을 나열합니다.
매칭 네트워크에 사용 가능한 저항기는 일반적으로 “1% 값”입니다. 2% 증분을 가진 공칭 값은 따라서 표 1의 Rs 및 Rp 값과 최대 ±1%까지 다를 수 있습니다. 네트워크 손실의 결과 오차는 Rs와 Rp가 표 1에서 반대 방향으로 벗어날 경우 가장 크며, 예를 들어 1% 저항 오차의 경우 N2 = 5에서 0.1 dB에 달합니다. 더 높은 정확도가 필요한 경우 그림 15 다음의 방정식에 실제 저항을 대입하여 손실을 계산해야 합니다.
저항기 정밀도에 대한 위의 논의는 트랜스포머의 삽입 손실 측정에 관한 것입니다. 두 매칭 네트워크가 동일한 한 진폭 밸런스는 저항 오차의 영향을 받지 않습니다.
| Z 비율, 1:N2 | Rs (그림 10) | Rp (그림 10) | 네트워크 손실, dB |
|---|---|---|---|
| 1:1 | 0.866 Rt | 0.683 Rt | 8.43 |
| 1:1.5 | 0.791 Rt | 1.291 Rt | 6.31 |
| 1:2 | 0.707 Rt | 2.414 Rt | 4.64 |
| 1:2.5 | 0.612 Rt | 5.56 Rt | 3.18 |
| 1:3 | 0.500 Rt | 없음 | 1.76 |
| 1:4 | 1.333 Rt | 2.000 Rt | 6.53 |
| 1:5 | 1.887 Rt | 1.581 Rt | 8.23 |
| 1:8 | 3.44 Rt | 1.265 Rt | 11.08 |
| 1:13 | 5.97 Rt | 1.140 Rt | 13.60 |
| 1:16 | 7.47 Rt | 1.109 Rt | 14.61 |
| 1:25 | 11.98 Rt | 1.066 Rt | 16.71 |